A (partially) failed attempt at improving the Transformer architecture.
Why it failed, explained at length. Nice cattle pictures as a bonus.
This post is a bit technical. I’ve tried to make it as simple as possible and to not hide a lack of intuitive understanding behind complex mathematical expressions. However, I believe it’s still fairly complex. By carefully reviewing this post, you'll gain a deeper understanding of key ML concepts. If you’re not familiar with the Transformer architecture, I strongly recommend 3b1b’s videos on the subject1. I made this post for people who like to dive deep into engineering problems and their (absence of) solutions. Please read the footnotes.
The final hidden state of a Transformer's channel – that is, the embedding vector after the last decoder layer – theoretically contains n_embd * 32 (or 16, depending on the configuration) bits of information. This is because it's composed of n_embd components, each encoded as a 32-bit floating-point number (fp32).
This final hidden state is then transformed into a probability distribution across all possible tokens. We sample from this distribution, resulting in a single token chosen from a vocabulary of vocab_size possibilities. The amount of information contained in this individual token can be quantified as log2(vocab_size).
The Llama 3-8B model has an embedding size of 4096 and a vocabulary size of 128,256. This means the unquantized last hidden state contains 4096 * 32 = 131,072 bits of information. However, this gets compressed down to approximately log2(128256) ≈ 17 bits when predicting the next token.
That's a significant reduction in information, which seems especially important considering that Transformers, as autoregressive models, rely on the generated tokens up to step n to predict the next token at step n+1.
Proposed architecture improvement: enriching token embeddings with the last hidden state of their generation step.
This idea sounded great, I was already picturing myself getting the Turin Award, making the Times cover and receiving a lot of emails from Altman, Amodei & al begging me to honor them by joining their companies. The Stateful GPT would give me fame, money and girls.
It turns out this wasn't as great an idea as I initially thought, for several reasons. The most obvious reasons are not the most critical ones.
1st Challenge: this is basically an RNN, so what about training parallelization?
When I first posted my idea on Reddit to get some feedback on this idea from people smarter than me, they all said “you’re basically re-inventing Recurrent Neural Networks. The exact architecture that was made obsolete by Transformers. Not good. A Transformer’s training can be parallelized, your architecture’s cannot.” It turns out they’re partially right on that, but only partially.
First, I’d like to take a step back and explain why RNN training is difficult to parallelize and why it matters. It is only loosely related to the main subject of this post but I find it interesting enough.
Why the training of RNNs is difficult to parallelize
I won’t dive too deep into how RNNs work, and as most blog posts do a very poor job at explaining them2, I’ll link a prompt I gave Grok. It did great, you can trust the answer. The core concept here is that in an RNN, to predict token n, you first have to predict all tokens up to n-1. So training an RNN on a text sequence of length n involves at least n sequential steps, each dependent on the completion of the last one. This is the exact opposite of parallelized training.
By contrast, a Transformer can be fed a n-length sequence and be trained to predict each token k from 2 to n+1 in parallel. If we take the training sequence '“the cat sat on the mat”, we get (6-1 =) 5 examples.
1. "the" -> "cat"
2. "the cat" -> "sat"
3. "the cat sat" -> "on"
4. "the cat sat on" -> "the"
5. "the cat sat on the" -> "mat"
These predictions can be performed in parallel thanks to the attention mechanism’s ability to handle variable context sizes and process each position's prediction independently (given the shared input). This ability is slightly hampered by my proposed architecture update, but we’ll see that later.
Now, you can actually parallelize the training of RNNs by using a large batch size: you can backpropagate through multiple full-sequences in parallel. The first problem is that the memory overhead is substantial: for each sequence, you have to store the whole, sequential, computation graph3 to then backprop through it. The second one, even worse, is that each sequence will still be processed sequentially.
Transformers’ computation graph, on the other hand, is quite light thanks to the absence of recurrence. And the only sequential thing about them is the layer-by-layer processing.
All in all, it’s more accurate to state that the training of RNNs is not very -yet still somewhat- parallelizable.
Why it matters
Although RNNs like LSTMs or GRUs are competitive with Transformers in terms of end loss (log-likelihood) vs. training compute (in flops), they are impractical due to their inability to make full use of GPUs.
In fact, if money could buy clock frequency (instead of more GPUs), Transformers wouldn’t have been needed: an RNN would train just as well (maybe even better?) than a Transformer on a single-core, 100THz CPU. But such a high frequency can’t be attained, for a bunch of reasons4. On the other hand, doubling compute power by doubling the number of transistors and logical cores is quite straightforward. Hence the need for a highly parallelized architecture.
Why the Stateful GPT’s training is still quite parallelizable
First, I’d like to give you a nice picture of Venice. It’s an incredible city and I’d like to visit it some day. I hitchhiked there once but I was in a hurry and had to go to Albania.

Back to the point.
Of course, the Stateful GPT behaves like a normal RNN during inference. As a consequence, its training should be difficult to parallelize.
Except if you accept a little discrepancy between what you train the model for and how you use it.
Here’s how the training goes, why it’s different from inference and why it doesn’t matter much.
Training:
Parallel Training Step: A standard, fully parallelized training step is performed on the Transformer. No information flows through the recurrent connection at this point. Cross-entropy loss (CE-loss) is computed, and normal backpropagation is performed. The last hidden states are stored.
Recurrent Training Step: The last hidden states stored in Step 1 are fed back into the model to enrich the token embeddings. Backpropagation is performed as usual, and new hidden states are stored.
Iterative Recurrence: Step 2 can be repeated multiple times, using the hidden states from the previous iteration, at the cost of additional training steps.
Here’s how training & inference differ:
Training: The recurrence depth is set to a fixed and finite number.
Inference: The effective recurrence depth is generated_sequence_length - 1. The first token is generated without recurrence. Token 2 uses Token 1's hidden state (1 degree of recurrence), Token 3 uses Token 2's hidden state (2 degrees of recurrence), and so on.
The discrepancy between training and inference is addressed by ensuring stability during training. If the CE loss remains controlled with increased recurrence depth during training, the model should be stable even with theoretically infinite recurrence depth during inference.
More formally, training ensures that CEloss(Tn)<CEloss(T0) for every recurrence depth n trained for. Otherwise, the model would just learn to ignore the hidden state information. Although it doesn't formally imply that this inequality holds even for recurrence depths not seen during training, it is empirically observed.
Empirically again, I could observe that a single recurrence step during training gives 95% of the gains I would get by using, say 10 recurrence steps.
I even made a little test, by encoding the training step’s recurrence depth and giving this information to the recurrent layer, so as to track the “optimal” norm of the token enrichment term vs. the recurrence depth.
The norm indeed grew with depth. This suggests that the Stateful GPT incorporates progressively more information into the token prediction as recurrence depth increases. The effect was very small, though: a 1% increase in average norm going from depth = 1 to depth = 3.
Of course, the compute-intensiveness of each training epoch is dependent on the recurrence depth: we set depth = 2 for example, we’ll have to make 3 forward/backward passes for each batch: 1 for the standard Transformer training + 1 for each recurrent step. Each epoch thus costs (recurrence_depth + 1) times more than for a standard Transformer.
We’ll see if that’s a problem.
For now, let’s check the architecture of the Stateful GPT.
A deep dive into the Stateful GPT architecture

Now it gets a bit technical.
The naive ways of enriching token embeddings with the last hidden state before their generation are either to:
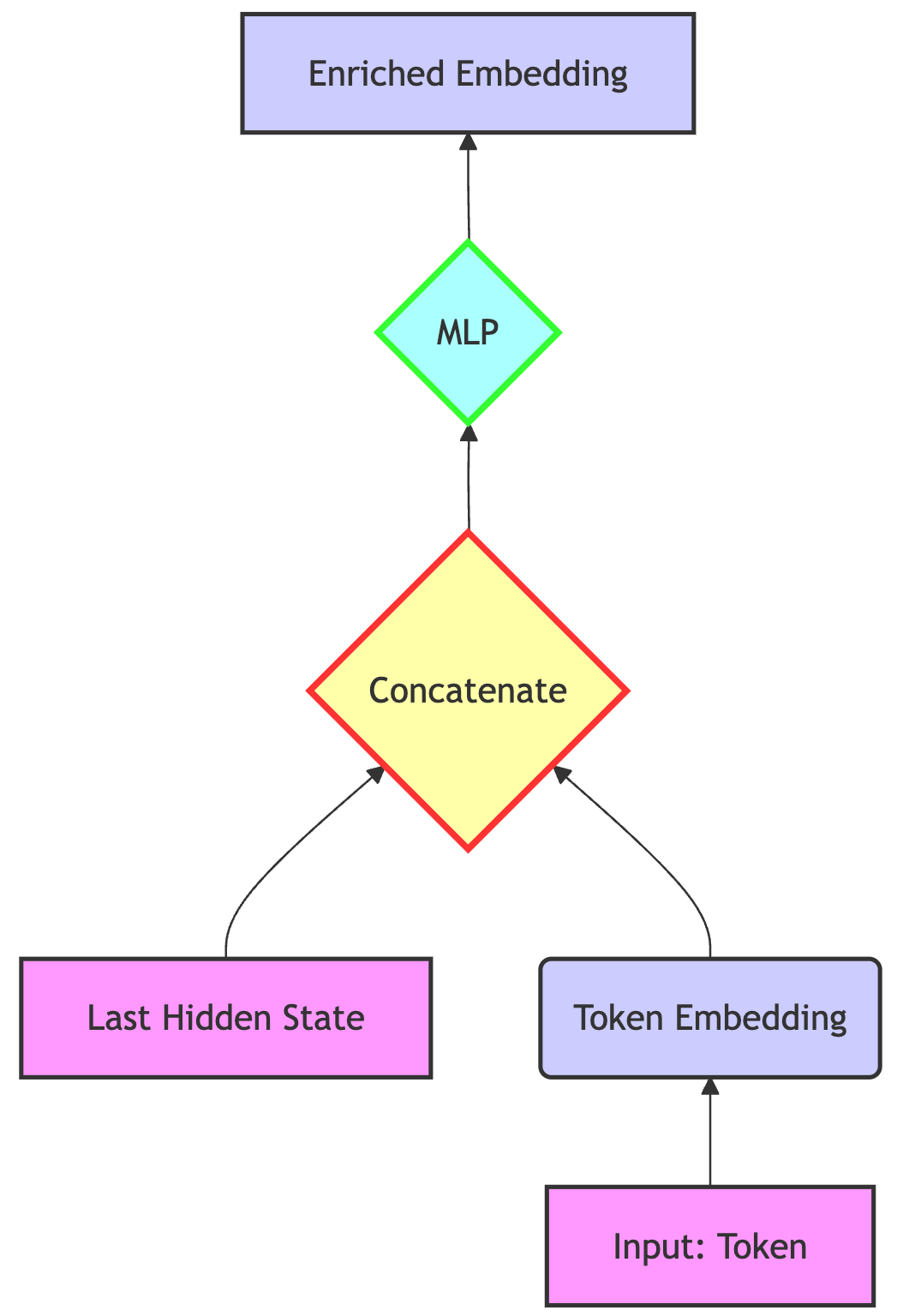
Concatenate the standard token embedding and the last hidden state, and down project / transform them back to a dim_embedding-sized vector.
Sum the standard token embedding and some transformation of the hidden state.
These two options are valid. The first one is more compute intensive than the second, as it deals with vectors of dimension 2*dim_embedding instead of just dim_embedding. On the other hand, it allows for a real interaction between the last hidden state and the token embedding. It’s not just blindly adding information.
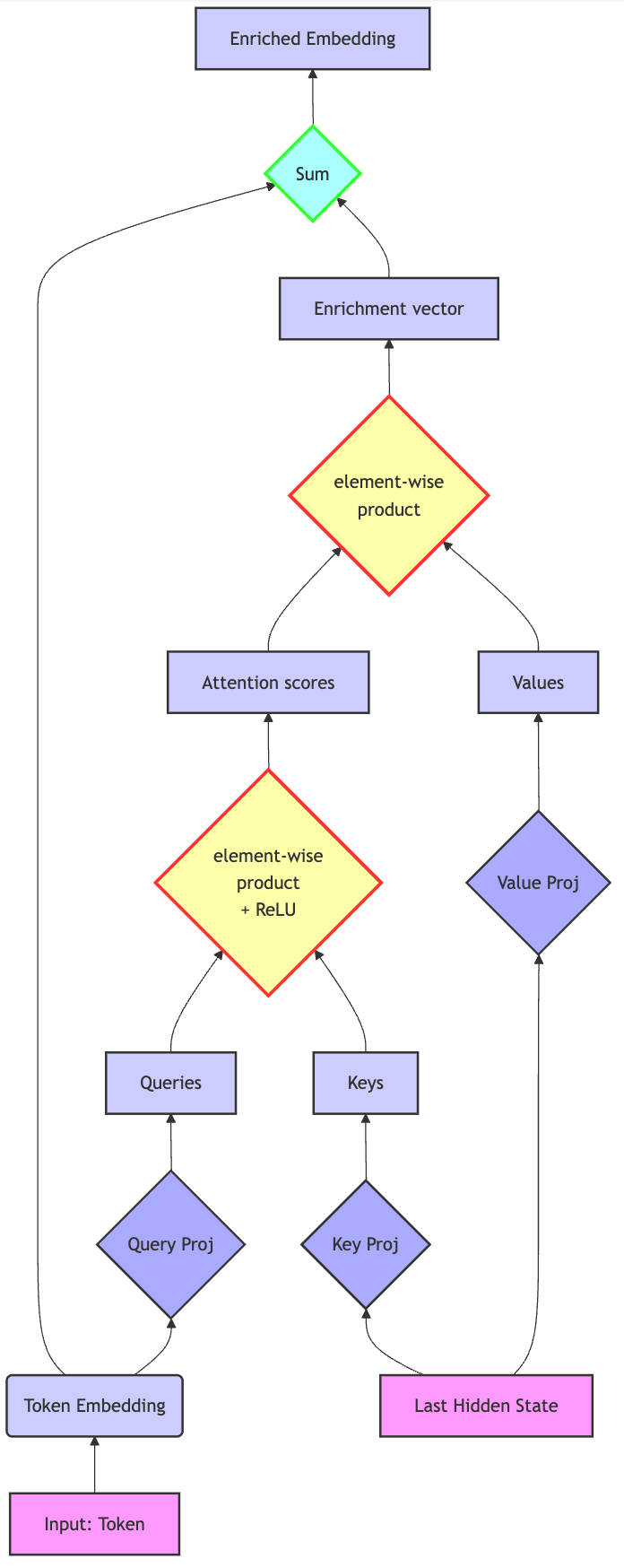
I decided to merge both approaches with a custom architecture halfway between the input gates of LSTMs and the attention mechanism of Transformers. The idea is to compute a component-wise attention score between the token embedding and the hidden state and update the former accordingly. From now on, I will refer to the token embedding as “x” and to the hidden state as “h”.
The high-level idea of this technique is to:
Check what information the hidden state can enrich the token embedding with. Compute an element-wise “attention” score that basically says, for each component, how much the token vector should be updated.
Project the hidden state into a space where it can be summed with the token embedding vector
Add the projected hidden state to the token embedding in order to enrich it. The sum is conditioned by the attention scores, meaning that the update’s magnitude will differ for each of the vector’s components.
So it goes like this:
More formally,
Let me explain this equation carefully.
So, each token embedding gets enriched (x = x + something) this way:
First, a learned matrix projects the hidden state into a nice (key) space where we can compute its element-wise affinity with the original token embedding. That’s the h@Wk part (in PyTorch, @ refers to matrix multiplication).
Second, a different learned matrix projects the token embeddings the same, into a “query” space. That’s the x@Wq part.
Then component-wise pseudo-attention scores are computed by multiplying each component of the projected token embedding by those of the projected hidden state. Let’s imagine x is the embedding of the word “car”. During learning, the query projection matrix has learned that this kind of tokens (nouns) are always willing to get their physical characteristics refined, for example by color or shape adjectives. So there will be high values for the components coding for “I want an update on my color, I have no idea what it is”. Meanwhile, the key matrix, through which the hidden state is projected, has learned to project the hidden state so that there is a clear “color” component. When you make a component-wise multiplication between the two vectors, you actually enable a dialogue like “Token embedding: I want my color updated, please.
Hidden State: I can definitely provide this information => high attention score for component ‘color’.
Token embedding: I’d like to know how fast I am.
Hidden state: sorry, I don’t know about that => low attention score for component ‘speed’.
Token Embedding: tbh, I don’t quite care about [something].
Hidden state: Too bad, I could have told you => low score.
Token Embedding: I don’t care about [some other thing].
Hidden state: Neither can I tell you about it => low score.”
In the equation, that’s the whole (h@W_k) * (x@W_q) term.
The negative scores are set to 0 by the ReLU activation function. This is not strictly necessary, but it doesn’t hurt performance and I like the increased interpretability it brings. Please note this example is anthropocentric and it doesn’t literally reflect what actually happens.So now, we have a component-wise affinity between the token embedding and the hidden state. We have to bring the information where it’s due. The hidden state is first projected by the Wv matrix into a value space (compatible with the token embedding), meaning that this projection tries to present the hidden state’s information in such a way that it can be added to the token embedding. If, for example, the color components of token embeddings are typically in position 29-31, but are typically in position 4, 8, 12 in the hidden_state vector, the Wv matrix will soon learn to have a 1 in positions (29,4), (30,8) and (31,12). Now that we have a nice projected hidden state vector, we just have to multiply it component-wise by the attention scores to get the enrichment term.
We just add this enrichment term to our initial token embedding.
That’s it. The rest of the Transformer is kept identical.
If you are familiar with attention, you may have noticed that this architecture is very similar to cross-attention, except that it’s element-wise, and not token-wise.
Let’s see how the it all performs.
Empirical results
As my goal was to test the idea as fast as possible, I chose to go with a character-level Transformer, to save a layer of complexity.
I trained all the Transformers on a Gutenberg 10MB custom dataset, comprising a few books stitched together. This dataset is deeply flawed: test and val splits are qualitatively different, as they likely don’t even come from the same book/author. But I decided not to care.
Different flavors of Stateful Transformer
Among the different possible designs for the token enrichment mechanism, the component-wise attention performs best, with the fewest parameter count.
The concatenation approach (shown in the first real figure) works nicely too, in terms of minimum loss vs. number of params, but its drawback is that you can’t easily turn off the recurrence: As you’re dealing with a MLP that takes both a hidden state and a token embedding (and outputs an enriched embedding), you can’t decide to just feed it a token embedding (and zero-pad the hidden state placeholder) and expect it to output a coherent token embedding.
Standard vs. Stateful Transformer
I first trained a very small and especially shallow Transformer5 for 40 epochs. Here is how the stateful Transformer (with recurrence depth = 1) compares to the standard one.
The Stateful Transformer’s run looks much better. And indeed it is: the Standard Transformer’s train loss after 40 epochs is reached only after 16 training epochs by the Stateful Transformer. It’s more than twice as fast, which means that, even accounting for compute overhead, it outperforms the Standard Transformer.
Interestingly, the stateful Transformer seems to be a bit more prone to overfitting. Indeed:
Meaning, in plain English, that the Stateful Transformer does not generalize as well as the Standard one. If you have any idea why, please tell me in comments. I have a few hypotheses, but none of them is fully satisfactory. By the way, the Stateful Transformer has 140,000 params and the Standard Transformer only has 128,000. That’s a difference of 8.6%, which is significant but unlikely to explain the difference in performance between the two architectures.
When I saw this kind of results, I thought the Stateful Transformer would work great. I believed it might even scale well, meaning that the performance upgrade would be even greater for bigger Transformers (see next section for more details).
In fact, it’s the exact opposite. The following is another training run, comparing loss vs. training epoch for larger Transformers (4 layers instead of 2, 950,000 params).
The stateful GPT here performs marginally better than the standard one. But it uses twice as much compute during training. In one word, it’s not worth it. When I figured this out, I used all available resources of intellectual dishonesty to make my stateful GPT work better. Maybe if I train it first without recursion and just fine-tune it on a few recursion epochs? Nope, doesn’t work. Well, it does, up to a certain point, but it’s not scalable. Maybe if I freeze all the weights except for the enrichment mechanism? Nope, doesn’t work either. I tested a lot of things but, at the end of the day, the compute overhead was just not worth it.
Is the train/val loss a valid metric?
By the way, you may be wondering if the train/val loss really is a good metric for performance, considering that the inference process is slightly different from the training process. To figure it out, I trained a “big” (5M params) on the same dataset to assess the output of these two small models.
Doing so isn’t as straightforward as it seems, as merely using the big model’s loss on text generated by the small models can be insufficient. Indeed, a string like “things of the street of the things of the street of the things…” is technically sensible (big model’s loss on this string is low), but its information content is very low.
So I wanted to assess both the information content of a text and its “sensibleness”, measured respectively by the compressed size of the text and the loss of the big model on it.
The randomness of a Transformer’s output grows with the temperature of its softmax.
Also, the compressibility of a string decreases with its randomness (a perfectly random string is impossible to compress).
Finally, the loss of a bigger model on text generated by smaller models grows with these smaller models’ inference temperature.
Below are some graphs showing some empirical results on this matter. I compared two models, a Stateful GPT and a standard Transformer, trained until they had the exact same validation loss.
What we can see here is that, for a given validation loss, the Stateful Transformer performs exactly the same as the Standard one, meaning that the validation loss is a valid proxy for the stateful model’s inference performance.
I think it’s time for another unrelated picture.

Why it only works for shallow Transformers
A delusional hope
At first, I thought my architecture tweak would work better for bigger Transformers.
The amount of information carried by an input vector depends on the transfer function of the network it is fed into. Quite obviously, if you take a dead neural net whose output is constant, you won’t be able to infer anything about the input. So, whatever the amount of information theoretically present in the input vector (32 bits * dim), you won’t be able to extract any.
Conversely, a big, well-trained neural network has a lot of decision boundaries, meaning that a small variation in the input vector will have a big effect on the output. I think the amount of information you can read from a vector is approximately equal to the number of decision boundaries of the NN, which is dependent on the number of parameters and the shape of the activation functions6.
Let’s keep this idea in mind: the bigger a neural net, the more sensitive its output is to small input variations.
Now, let’s look at something else: in a Transformer, the vocab size is finite, and so is the embedding dimension. When you embed tokens (the first thing you do in the forward pass of the Transformer), you look up the token id in a dictionary and get its associated vector. So, in the continuous vector space of dimension n_embedding, you only have a discrete set of vocab_size vectors you can feed the Transformer with. And I thought that the Stateful Transformer’s usefulness was in padding this discrete set to make it more continuous.
And I thought that this padding effect would be especially beneficial if the subsequent Transformer has the complexity to make use of the additional precision. Namely, if it’s bigger.
Also, if you look closely, the size of the gaps in the token embeddings space usually grows with the size of the model: the average distance between closest tokens grows like78
Anyway, two good reasons to believe, at first sight, that the Stateful Transformer architecture would perform better on big Transformers.
It doesn’t.
Reality strikes back
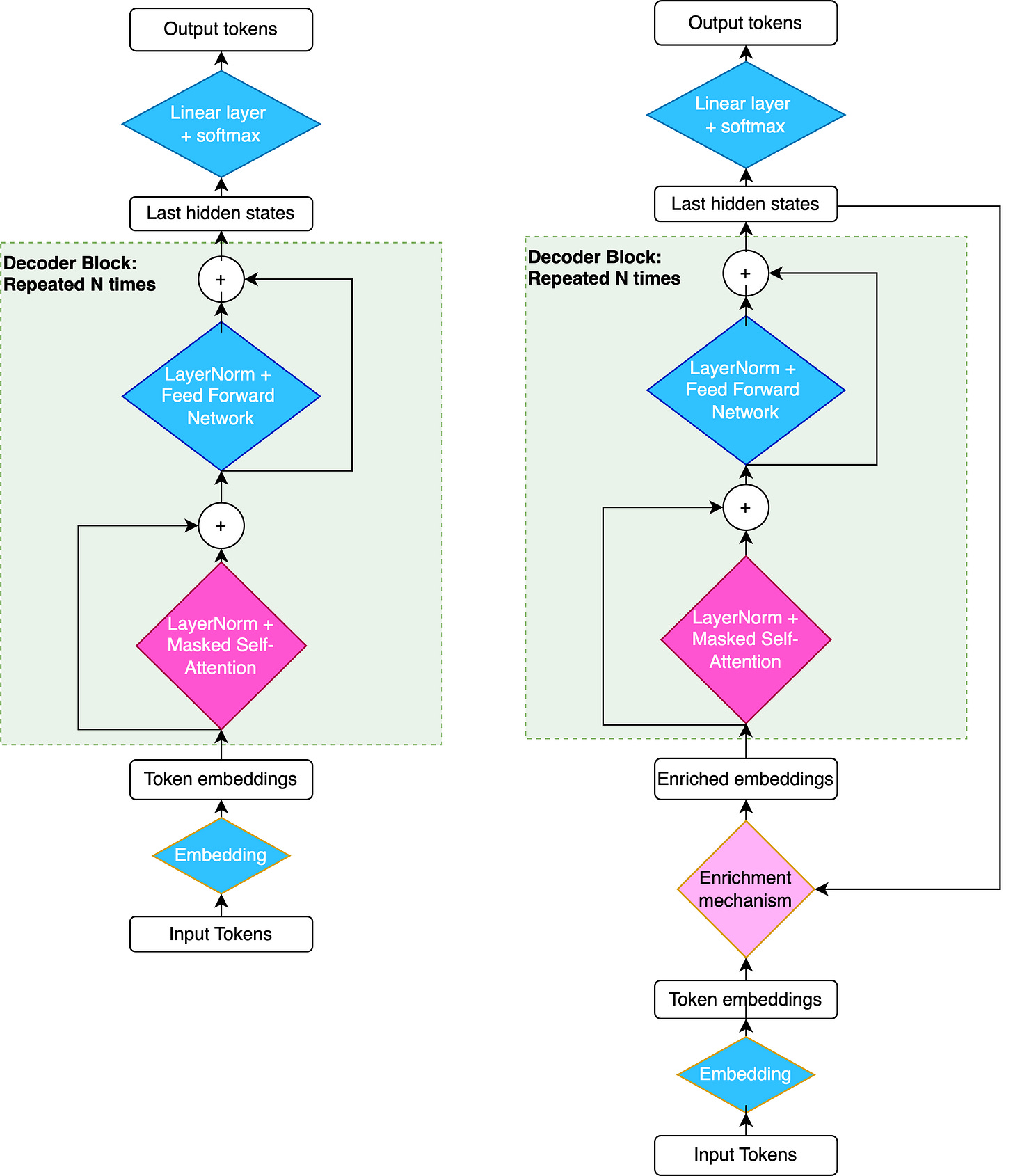
Let me show the architecture again:
All the blue steps here are steps where token embeddings are processed in parallel, with no communication between them.
The pink steps, conversely, are steps where each token vector gets updated based on the other tokens. Best example for that is attention.
I decided to give the enrichment mechanism a light pink tint, as the n-th token’s embedding is updated based on the (n-1)-th last hidden state (which was actually the one used to predict the n-th token). So, technically speaking, there is some token-to-token interaction happening, but it’s both local and unidirectional.
What’s interesting is that token mixing happens in each decoder layer. Let’s take a 50 layer-deep Transformer, trying to predict the n-th token of a sequence. As they flow through the Transformer, all the previous tokens’ hidden vectors provide information to the n-th token’s vector, through the attention mechanism. So, the (n-1)-th token’s penultimate hidden state freely provides information to the n-th token. As for the very last couple of hidden states (after the last attention layer), they don’t, because there are no token-mixing steps left.
What it all means is that the Stateful Transformer’s architecture update is interesting only in that it allows the very last hidden state of token n-1 to provide information to token n’s embedding, instead of the penultimate hidden state. Of course, the communication medium between vectors is completely different for these two cases9, but the end result is the same: tokens communicate up to the last layer in the standard Transformer, while the Stateful Transformer goes the extra mile and allows the tokens to communicate after the Feed Forward Network part of the last decoder layer. This update is really just about not discarding the work done by the last FFN on the previous token embeddings: the work done by all previous layers is still available thanks to the attention mechanism.
And this extra mile is not that valuable.
Intuitively, the last hidden state doesn’t carry much more information than the penultimate hidden state if there are a lot of decoder layers: each layer (including the last one) loses importance when there are a lot of them10.
So, this is the reason why the stateful Transformer architecture tweak only works for shallow models.

Conclusion:
This architecture tweak sucks, like nearly every other Transformer “improvement”.
Maybe you’re not convinced that “the last layer of a Transformer isn’t that important if there are a lot of them”, I wasn’t either. But upon closer look, if it’s indeed important, why not just add one more layer? It will do the same job as the recurrent architecture trick, while being more straightforward to train and use.
My next post will either be about some things I learned when researching this idea11, or a credit scoring model I’d like to train.
Only one little error here: Attention head results are concatenated, not summed. But technically, you could argue that a concatenation of vectors is equivalent to the sum of their expanded (ie. padded with 0s) version, so it’s just a slight imprecision.
In what fucking world do their authors live to believe that their readers will enjoy a bunch of formulas full of unspecified terms at the beginning of a “RNNs simply explained article”? Most of them go from “Here is the very high level idea (so high-level it doesn’t tell anything)” to “So, h_t = f(W * h_{t-1} + U * x_t + b) and y_t = g(V * h_t + c)”.
Backprop is basically about moving the parameters of a model in the direction that makes them decrease the loss. So, first, you have to compute the gradient of the loss w.r.t the parameters. You could use the finite difference method (the (f(x+h) - f(x)) / h stuff) along with the chain rule, but it’s very inefficient. So all ML frameworks store the computation graph of the network to be able to tell things like “the input was transformed in such and such way when going through the neural net, so the gradient of the loss w.r.t each layer’s params is such and such”.
First, the Field Effect Transistors used in integrated circuits act like capacitors. Meaning that switching them on and off involves a transfer of electrons which potential energy is equal to their capacitance multiplied by the voltage squared. This is just lost energy and heat. This lost power/heat is proportional to the rate at which you turn these transistors on and off, aka the clock speed. Heat management is one of the hardest problems of chips. Second limit is just the speed of electricity, which is approx 10⁸ m/s in silicon. A 100THz chip would need the signal path lengths max deviation to be less than 1 micrometer to ensure correct computations.
n_embd = 64, n_heads = 8, n_layers = 2, block_size = 33, batch_size = 2048
If I were to make a guess, I’d say that, for a MLP with ReLU activation the number of decision boundaries is basically lower than or equal to (2*dim)^depth, assuming that the dim is constant.
Think of a chess board: the closest distance between two neighboring cells is
Meaning that if you had 2-dimensional embeddings with a vocab size of 64, the average distance between two neighboring embeddings would be about one eighth of the maximum norm of these embeddings.
In fact, for practical model sizes, the average min distance between neighboring embeddings is terribly close to their norm. Meaning that they are as distant as can be. A surprising consequence of the curse of dimensionality.
Global attention between two token’s equally high-level hidden states vs. enrichment of a low-level token embedding with a high-level last hidden state.
Especially when you account for the “curse of depth” in LLMs
Namely:
1) how the Fourier transform of the activation function used in an NN relates to the Fourier transform of the NN’s prediction surface. Or, put more practically, why you shouldn’t use ReLUs when approximating a low-frequency function and conversely shouldn’t use GeLUs when modeling highly discontinuous phenomena.
2) When a higher hidden dim is needed vs. when a deeper network works best
3) Why and how the function to model conditions the shape of the best_attainable_loss vs. number of layers curve.